
“[M]ultiplicities specify the structure of spaces of possibilities, spaces which, in turn, explain the regularities exhibited by morphogenetic processes.”
– Manuel DeLanda, Intensive Science and Virtual Philosophy
In the work of French philosopher Gilles Deleuze, multiplicities make up one of his most important, yet widely misunderstood concepts. A fascinating approach to both epistemology and ontology, the fields that deal with how we know what we know and what it means to be respectively, multiplicities offer a totally new way of looking at the world. However, reduced down to its regular definition as a synonym for ‘many’, the very nature of the concept – borrowing as it does from differential geometry, dynamical systems theory, and group theory – is oftentimes lost. In this article, I hope to outline some of its main features, taking largely from Manuel DeLanda’s book Intensive Science and Virtual Philosophy.
The article is split into four sections: the first explores the purpose of the concept and its basic aspects, the second examines its role in the philosophy of Henri Bergson as understood by Deleuze, the third discusses the ways in which multiplicities can be used in theory, and finally the fourth describes what it means for multiplicities to specify ‘the structure of spaces of possibilities’ as described by DeLanda.
Manifolds and Essences

“[A]lways there is the selection from among claimants, the exclusion of the eccentric and divergent, and this in the name of a superior finality, an essential reality...”
– Gilles Deleuze, Plato and the Simulacrum
As Deleuze and his collaborator Félix Guattari state in their 1991 book What is Philosophy?, philosophy is first and foremost the production of concepts. These concepts always have a reason for being and multiplicities are no exception. Simply put, they are Deleuze’s response to the problem of identity. More specifically, they replace the notion of essences – those irreducible properties that make a thing a thing. To understand why this replacement was necessary, some background on Deleuze would be well worth it.
Born in 1925 and dying in 1995, Gilles Deleuze can be described in a multitude of ways – as a pure metaphysician, a transcendental empiricist, and a philosopher of difference, to name a few. However, he was also a process philosopher. Following Nietzsche, Bergson, and Whitehead, Deleuze conceptualised the world in terms of a complex web of processes, becomings, and shifting relationships. In his ontology, there is no such thing as a truly stable object. Instead, there are only the metastable results of interacting flows, always at risk of falling into chaos. It’s from this dynamic point of view that essences – conceptualised as static and unchanging – fall short.
Concerning identity, Deleuze takes a morphogenetic approach, focusing on the processes that give rise to specific forms. Everything has a history and everything is in flux, thus requiring a much more flexible approach than that offered by essences. It’s here that multiplicities come in. Instead of forming systems of rigid designations like is done in essentialism, they chart how identities change and become different over time. Now understanding the why behind the concept, we can get into the specifics of the what.
Gilles Deleuze

“In the beginning, there is the chaos of unformed and unstable matters that flow freely as so many mad particles or intensities. This is the first of the set of ‘first principles’...”
– Ian Buchanan, Assemblage Theory and Method
To begin with, the notion of a multiplicity is based in mathematics – more specifically, in differential geometry. The term has a rich history, having entered into Deleuze’s lexicon via fellow French philosopher Henri Bergson’s translation of Mannigfaltigkeit, a word coined by the German mathematician Bernhard Riemann that is most often rendered into English as manifold. However, before we get ahead of ourselves, understanding some of the basics of differential geometry is necessary to properly grasp the nature of these structures.
As the name implies, differential calculus concerns differences, or, more precisely, the rate of change between one quantity and another. Differential geometry was born when mathematicians began to apply this framework to objects like curved lines and spaces, where the rate of change took the form of measuring curvature. What is important for us now is the work of Carl Friedrich Gauß, who found that the curvature of two dimensional surfaces could be studied without having their axes embedded in a three dimensional space.
To break this down, Cartesian geometry traditionally considered curvature only in relation to the enveloping space in which the curved surface exists. Intuitively, this might seem the only way of doing things: how can something be curved without being relative to something else? However, Gauß – through differential calculus – was able to find a way of studying curvature locally, taking distances, angles, and rates of change as his bearings. In other words, he showed that surfaces could be treated as spaces in their own right, defined intrinsically rather than extrinsically. Manifolds took shape as Riemann began applying this idea of intrinsic definition to n-dimensional spaces and surfaces – general structures with variable dimensions.
Bernhard Riemann

“[Gauß] advanced the totally new concept that a surface is a space in itself. It was this concept that Riemann generalized, thereby opening up new vistas in non-Euclidean geometry.”
– Morris Kline, Mathematical Thought: From Ancient to Modern Times
When it comes to their relationship with differential geometry, Deleuzian multiplicities share these properties with manifolds. Concerning their intrinsic definition, this makes them immanent. In stark contrast to transcendent essences, which act to instil a totalising unity from without (i.e. extrinsically, like an n+1 enveloping space), multiplicities exist purely through themselves. Looking now at the notion of multiplicities having variable dimensions, this is where dynamical systems theory comes into play.
Essentially, applied to dynamical systems theory, each dimension of a manifold corresponds to the space of possibilities of a degree of freedom — the ways in which a given object can experience change. DeLanda gives the example of a pendulum, the degrees of freedom of which consist of momentum and velocity. In order to plot them, the pendulum’s manifold is two-dimensional. Going further, more complex things — for example, bicycles — can also be explored through manifolds, the five main parts that compose them each having the same two degrees of freedom as the pendulum for a total of ten dimensions.
Overtime, changes in a given manifold’s degrees of freedom can be used to construct a path or trajectory. This makes it possible to capture a process – hence the dynamic part of dynamical systems theory. These trajectories don’t exist in a bubble, however. Instead, they are organised around what mathematician Henri Poincaré termed singularities – a notion appropriated by Deleuze. A singularity, a deeply complex concept in its own right, refers to a kind of processual tendency with certain features that allow it to act as an attractor, causing trajectories that fall into its sphere of influence to end up at a certain point. To differentiate this seemingly fatalistic quality of multiplicities from essences, it’s here that group theory becomes important.
Clocks with their pendulums

“The sweep of the pendulum had increased in extent by nearly a yard. As a natural consequence its velocity was also much greater. But what mainly disturbed me was the idea that it had perceptibly descended.”
– Edgar Allen Poe, The Pit and the Pendulum
However, before we get to that, something underlined again and again by Deleuze in his work on singularities is that they are necessarily topological – not geometric. What this means is that singularities – as points on a manifold – produce the conditions for certain forms, but remain distinct from their actualisation. Topological here refers to the non-quantitative nature of singularities, whose actualisations are metric and thus geometric. To give an example, take soap bubbles or crystals of salt. They both involve the same kind of singularity – the attractor that gives rise to them is a point of minimal energy –, but remain completely different in their geometry. This can again be contrasted with essences, which rely – in the case of the soap bubble – on some sort of geometric ideal of sphericity.
Turning now to the place of group theory in multiplicities, its role is to illustrate the unfurling nature of singularities. Opposed to the clear structures implicated in essences, multiplicities are much more fuzzy – at least on the surface. The singularities that structure them come in sets, but their individual elements aren’t immediately obvious: instead, they ‘progressively specify the nature of a multiplicity as they unfold following recurrent sequences,’ to quote DeLanda. In other words, a multiplicity contains an obscure structure that only develops over time, similar to what happens in eggs during embryogenesis (processes unfurling according to obscure zones of biochemical concentration, for instance).
Group theory enters the frame as a way to explore how sets of singularities interact. Here, some definitions would be helpful – starting with that of group theory itself. A subfield of abstract algebra, it is focused on the study of groups, sets of entities with a determined rule of combination and specific properties like closure. Whilst rules of combination concern things like subtraction, addition, and so on, closure describes the ability for the combination of entities in a set to produce another of its elements. For example, positive integers form a group under addition, since adding any of them together always results in another positive integer.
Trajectories following attractors
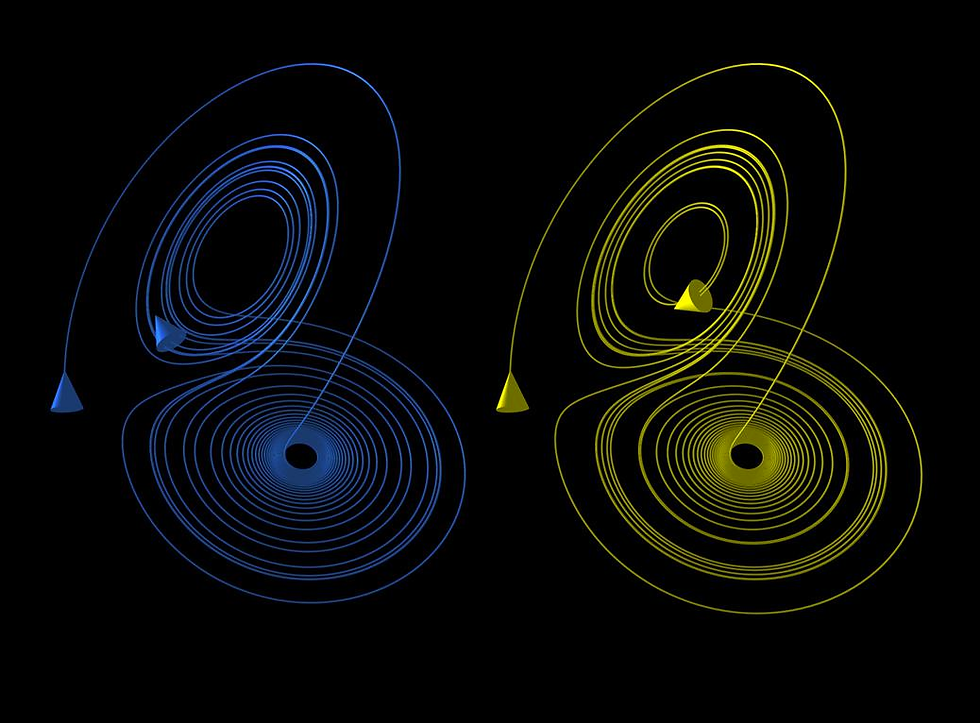
“The dynamics of singularities always result from a small miracle, encounters that may trigger transformations that are no longer singular, since they can upset the entire planet.”
– Félix Guattari, Soft Subversions
However, for Deleuze, groups of transformations are much more interesting than those of objects. An example of such a group is a set of 0, 45, 90, 135, 180, 225, 270 and 315 degrees, all of which undergo 45° rotations. Applied to geometric forms, it is possible to use this group of transformations to measure degrees of symmetry: a cube rotated 45 degrees perceptibly changes, but a sphere doesn’t. By classifying objects in this way, the focus shifts from some inherent thingness onto the dynamic events that influence their features. Additionally, this framework can be used for analysing symmetry-breaking transformations, for which Deleuze uses the term bifurcations.
By comparing entities undergoing the same group of transformations, it’s possible to picture a process whereby one can be converted into the other. For example, a transformation that breaks the sphere’s symmetry can result in a cube. To give a more concrete example, take water. When it undergoes low temperatures, it transforms into ice. Likewise, undergoing high temperatures transforms it into steam. Both instances involve the water’s symmetry being broken. When it comes to bifurcations in multiplicities, they involve the symmetry-breaking transformations of singularities. Maybe one singularity becomes unstable and breaks into two, or a collection of them periodically transforms back and forth between different degrees of symmetry. It’s for this reason that they are described as unfurling or unfolding.
Multiplicities additionally have what is known as mechanism-independence. Their bifurcations aren’t impacted by outside factors, like cause and effect, but their actualisations are. They are universals, but not in the abstract, general sense of essences. Like we saw in the example of the soap bubble and salt crystal, they both have the same topological singularity or general property (a point of minimal energy), but their geometric actualisations are completely divergent as a result of how that singularity’s bifurcations are realised. In other words and to quote DeLanda again, ‘multiplicities give form to processes, not to the final product, so that the end results of processes realising the same multiplicity may be highly dissimilar.’
Bergsonism and Duration

“[W]hen I replace myself in duration by an effort of intuition, I immediately perceive how it is unity, multiplicity, and many other things besides.”
– Henri Bergson, Introduction to Metaphysics
So far, we’ve examined some of the mathematical qualities associated with multiplicities, but what about their philosophical implications? In this section, I hope to apply some of the ideas discussed in the last section to Deleuze’s reading of Henri Bergson, found in the prior’s 1966 monograph Bergsonism. This will serve to strengthen the bridge between manifolds and multiplicities and to set the groundwork for Deleuze’s own innovations on the concept, which will be explored in more depth in the next section. However, before that, it would be helpful to know a little bit about Bergson.
A metaphysician born in 1859 and dying in 1941, Henri Bergson’s legacy is a complicated one. Whilst essentially a rockstar of early 20th century French philosophy, being awarded the Nobel prize for literature and consistently drawing massive crowds to his public lectures, his influence almost entirely dried up during the post-WW2 era up until the publication of Deleuze’s book. The reason for this fall from grace was largely rooted in his method. Whilst science was becoming increasingly popular for explaining the nature of reality, Bergson instead insisted on the importance of intuition over rationality. Although the latter had its place, Bergson argued that it is entirely incapable of explaining objects absolutely – instead, rationality (or rather, analysis) can only grasp things relatively.
To give quite a simplified account of his argument, this can be pictured with the example of picking a book off a shelf. Intuitively, we are able to grasp the action as it happens in its totality – a hand moves from A to B. However, if we try to analyse the action, we immediately run into problems. Analysis necessarily consists of dividing it into certain symbols, like centimetres or inches travelled, but these symbols are always relative. Centimetres can be broken down further into millimetres, micrometres, etc. Bergson says that all analyses are thus analyses ad infinitum: they get bogged down in Zeno’s dichotomy paradox, never being able to fully understand the object they seek to grasp and instead necessarily distorting it.
Edited image of Deleuze in front of two Bergsonian memory cones

“Intuition is a method of feeling one's way intellectually into the inner heart of a thing to locate what is unique and inexpressible in it.”
– Henri Bergson, Introduction to Metaphysics
A final distinction that I’ve only alluded to up until now, but which is very important to understanding Bergson and multiplicities, is that between the virtual and the actual. These are massively complicated concepts in Deleuze’s work, but for our purposes, they can be quite bluntly simplified as the realm of ontological problems and the realm of their solutions respectively. In Difference and Repetition, an example Deleuze gives is of the eye. The virtual problem it solves is the need for an animal to respond to light (e.g. in order to position itself in its environment or to find food). The eye is an actualisation of this virtuality, the elements that give rise to its existence – elements that are no less real than the actual entity they give rise to. As a small aside, the virtual and actual only exist through their relationship; they are interdependent.
It’s important to stress again that this is a very rough approximation, but I hope it’s clear enough to connect them to what we’re talking about here. The two are very important to Bergson, for whom – following Riemann – there are thus two types of multiplicity: virtual continuous multiplicities and actual discrete multiplicities. As a final disclaimer, not all of what we discussed in the last section applies to Bergsonian multiplicities – especially when it comes to singularities and bifurcations, which, to my admittedly meagre knowledge of Bergson, don’t appear in his work. However, even if Deleuze’s conception of multiplicities is more heavily influenced by mathematics compared to Bergson’s, there is still a massive overlap between the two.
With that out of the way, what purpose do multiplicities serve in Bergson’s work? According to John C. Mullarkey in his 1995 article Bergson’s Method of Multiplicity, there are three main principles that structure Bergson’s understanding of space: ‘space is a derivative of movement; all movement is action; and secondary qualities have an objective, spatial existence.’ Multiplicities come into the equation as a way of exploring the differences between movement (continuous and virtual) and space (discrete and actual). In order to outline the features that these multiplicities contain, the rest of this section will focus on Bergson’s division between duration and objective time.
Artistic rendering of two black holes

“[W]e shall no longer consider states of consciousness in isolation from one another, but in their concrete multiplicity, insofar as they unfold themselves in pure duration.”
– Henri Bergson, Time and Free Will
Bergson’s continuous multiplicities have a number of defining features. Namely, they’re qualitative, divisible only in kind, subjective, successive, virtual, and – perhaps most importantly – temporal. In Bergson’s eyes, duration is essentially the continuous multiplicity from which everything else is actualised. To put it simply, it refers to a form of lived time only graspable through intuition. It’s a continuous flow, with no symbols truly delineating the past from the present. In other words, duration is time as pure movement.
Beginning with the first three characteristics that define continuous multiplicities (quality, division in kind, subjectivity), they are all closely intertwined. In the case of duration, it is qualitative in the sense that you can’t have more or less of it. There’s no such thing as experiencing one moment more than another. Instead, there are only different kinds of moments influenced by memory. The swinging of a pendulum, for example, is qualitatively different through duration as different swings take on new significance based on prior ones. In this way, duration is divisible in kind. This form of time is subjective; in the words of Deleuze, we always discover ‘other durations that beat to other rhythms.’ In another sense, Bergson’s distinction between objective and subjective can be boiled down to that which is knowable through intuition (the latter) and that which is knowable through analysis (the former). With that, we can look at the other three qualities.
What does it mean for time to be successive? Essentially, this is what distinguishes it from space: succession is simply the continuous part of continuous multiplicities, where it denotes movement or – more specifically – a temporal flow. To quote Bergson on duration, it is ‘the form which the succession of our conscious states assumes when our ego … refrains from separating its present states from its former states.’ One moment is succeeded by another, a phenomenon without which duration wouldn’t be able to durate in the first place. Having tackled succession and temporality, we can now look at duration’s virtuality. Basically, linking to our earlier definition of the virtual being the realm of problems, duration is such insofar as it is constantly being actualised into objective time.
An old clock

“The clock [is] a technical machine for measuring uniform time, and [is] a social machine for reproducing canonic hours and for assuring order in the city.”
– Gilles Deleuze & Félix Guattari, Anti-Oedipus
With this, it’s time to turn our attention to their discrete counterparts. These are defined by Bergson as being quantitative, divisible in degree, objective, coexisting, actual, and spatialised. Objective time, also known as mathematical or scientific time, is a great example of all these elements. It’s the form of time that occurs through analysis rather than intuition, reduced down to symbols like seconds, minutes, and hours (hence being objective). In other words, this is the sort you find on a clock or in a calendar.
For this concept, I would like to start with what it means for time to be spatialised. Basically, we have a tendency to analyse time as being some sort of 4th dimension. In this dimension, moments are separated from each other based on their location on a timeline. Unlike with the succession of duration, these points simply coexist – nothing durates, time just lurches from moment to moment or point to point. Because of this spatial nature, objective time can be quantified and divided in degrees. Seconds play the roles of centimetres, minutes – the role of metres, etc. These measurements can be broken down into smaller and smaller units (analysis).
However, this form of time can’t exist by itself. Rather, it is a reflection (or rather, an actualisation) of the lived time found in the continuous multiplicity of duration. The problem posed by virtual duration is how to analyse it and the answer is to make it undergo spatialisation. This particular conceptualisation of time is problematic for a number of reasons (e.g. it abstracts the lived experience of duration), but it serves a purpose. It takes a subjective, almost impossible to conceptualise thing – the continuous multiplicity of duration – and translates it into an objective form. As we’ll see in the next section, this is similar to how actualisation in Deleuze transforms n-dimensional multiplicities into things that can exist in our 3D space.
A prism producing a rainbow

“Intensive physical properties, such as temperature or pressure, produce extensive physical properties, such as length, area, volume or entropy.”
– Alan Boardman, Carbon Monochrome
Although Deleuze had not yet developed his specific understanding of the two terms when Bergsonism was published, a useful division to make at this point is between intensive and extensive properties. In thermodynamics, these properties usually refer to those that do not depend on the amount of material in a given system and those that do respectively. For example, temperature is intensive, but mass is extensive – no matter how much of the same material you take away, it’s still going to be, say, 50° centigrade, but its weight will change. Deleuze takes this distinction and goes a step farther by saying that intensive properties are those that differ in kind from each other, whilst extensive properties differ in degree.
In this way, continuous multiplicities like duration are intensive, whilst discrete multiplicities like objective time are extensive. If we return to the quote by Mullarkey, he states that secondary qualities are spatial – in other words, that they’re extensive. This idea of extensive properties being second to intensive properties (intensities, as Deleuze often calls them) is important to grasping Deleuze’s understanding of actualisation. The intensities that make up duration – its heterogeneous strands – are what give rise to the spatialised, extensive objective time of scientists and mathematicians. However, as a small aside, Bergson himself was opposed to this use of intensity – something Deleuze explores in Bergsonism.
To wrap up this section, we looked at two types of multiplicities and their relationship through the lens of time and space. In the process, we saw how primary qualities implicated under continuous multiplicities lead to the production of secondary qualities in the form of discrete multiplicities – the theme of which will be the focus of next section. Additionally, we explored some very important distinctions that Deleuze would continue in his own work, like that of the virtual versus the actual, the intensive versus the extensive, and difference in kind versus difference in degree.
Difference and Ideas

“Multiplicities are rhizomatic, and expose arborescent pseudo multiplicities for what they are. There is no unity to serve as a pivot in the object, or to divide in the subject.”
– Gilles Deleuze & Félix Guattari, A Thousand Plateaus
Having detoured through Bergson, it’s now time to apply multiplicities to the philosophy of Deleuze himself. In particular, I would like to examine their role in relation to one of his most important works: his 1968 Doctorat d’Etat thesis Difference and Repetition. From it, I hope to offer some concrete examples of what he terms Ideas (another name for multiplicities).
It’s difficult to overstate the importance of this work. Despite only being his first foray into developing a philosophical system of his own, Deleuze considered it to be his magnum opus, often remarking that the rest of his work was simply an extension of the core ideas laid out in the thesis. One of those core ideas is the problematic nature of representation, which Deleuze sought to challenge through championing a philosophy of difference in itself. With this, it would be worthwhile to further explore Deleuze’s opposition to essences and essentialism.
To demonstrate what exactly an essence is, take a drawing of a cat. In an essentialist framework, it is such only as a degraded representation of the perfect, abstract idea of a cat. For Deleuze, this way of looking at ontology is highly problematic for reasons deeper than simply being static. Namely, it essentially presupposes itself: the representation found in the drawing is explained as a deformed copy of an ideal, but what gives form to that ideal? Essentialism simply kicks the can down the road. To attempt to avoid falling into this trap, Deleuze suggests that we have to begin with the concrete and work up to the abstract, not vice versa. This is the backdrop on which he develops Ideas.
Plato, Deleuze, and Bergson

“There is neither identification nor confusion within the Idea, but rather an internal problematic objective unity of the undetermined, the determinable and determination.”
– Gilles Deleuze, Difference and Repetition
What Deleuze means when he says that Ideas are concrete universals – as we touched on earlier – can best be appreciated using the example of colours. As Bergson lays out in his last work, The Creative Mind, published in 1934, there are two ways of approaching what makes a colour a colour: 1) you can create an abstract essence by removing from red what makes it red, from blue what makes it blue, and so on; or 2) you can bring them all together to produce a ‘pure white light’, compared to which the differences between colours are all the more brilliant.
To understand how the Idea of colour is concrete in the second example, compare it to the essences in the first account. In the case of essentialism, there is a general ideal under which all the colours are subjected – an n+1 enveloping space, like discussed in section one. However, in the case of the Idea, all colours coexist within it. There’s no overarching totalising unity, no enveloping space. Rather than a question of deformed representation, the focus is instead on a process of actualisation and individuation. The differences in kind between each colour is maintained inside the Idea itself. In other words, the Idea’s domain is fully immanent.
This takes us to the distinction between continuous and discrete multiplicities in Deleuze’s work. These aren’t terms he himself uses regularly, but they are useful for conceptualising how virtual multiplicities are different from actual ones. Essentially, like I said in the first section, Ideas are fuzzy – they tend to blend into one another, forming something of a mesh or continuum. There is often quite a bit of overlap between different Ideas, like the singularity of minimal energy found within both the Idea of salt crystals and the Idea of bubbles. Discrete multiplicities occur when this continuum is progressively cut up into the much simpler space we occupy. It’s this that most of the rest of this section will focus on.
Three paintings by Francis Bacon

“The virtual is a differentiated and differentiating process whose differentiating dynamism coincides with its differenciated actualisation.”
– Constantin V. Boundas, What Difference Does Deleuze’s Difference Make?
Something that crops up throughout D&R is the division between differentiation and differenciation. The purpose of this small typographic distinction is to illustrate the ways in which difference functions differently in the virtual versus the actual. Essentially, differentiation refers to the virtual process of unfurling bifurcation that we discussed in section one, whilst differenciation describes the actual process that gives rise to discrete multiplicities. To borrow from DeLanda yet again, opposing transcendent essences, which exist in a dimension separate from ours, ‘Deleuze asks us to imagine a continuum of multiplicities which differenciates itself into our familiar three-dimensional space’.
This idea of difference being a force of actualisation can be found in Bergsonism, where Deleuze reworks Bergson’s concept of élan vital. Originally conceived as a kind of creative life force, Deleuze reconsiders the notion as a process of progressive differenciation involved in evolution. Opposing preformism, the belief that species change in such a way as to realise some sort of potential (not unlike an essentialist perfect form), Deleuze stresses the fact that evolution is instead productive. It creates and introduces difference: that between plants and animals, then that between intelligence and instinct, etc. Through the élan vital, the mesh of virtual multiplicities that produce the conditions for life is progressively cut up into discrete chunks, producing actual forms.
Differenciation functions very similarly to differentiation, also progressing through cascades of symmetry-breaking transformations. However, unlike its virtual counterpart, it is not mechanism-independent: its process is linked to outside factors such as causality, producing qualities and quantities as bodies interpenetrate. For example, the Idea of a given species is actualised through evolution or the élan vital in relation to its environment. Perhaps to thrive, it needs to be a certain length, like in the case of a giraffe. The lengths of the necks of successful giraffes differenciate themselves from those of less successful ones through natural selection, a process of causality (long necks = more food = more fit) governing the process.
Meteorological map of the US illustrating intensities

“Intensity is dynamism, it is a flow of variable strength and of differential processes, chiefly tied to sensation, but also to forms and concepts, and connected to becoming.”
– Paolo Bertetto, Concept, Sensation, Intensity
To give a more concrete example of what an Idea might look like and how it might be actualised, hurricanes offer a fantastic case study. Although perhaps too difficult to work out how many dimensions their virtual multiplicity contains, they are structured by a myriad of intensities, such as temperature and pressure. The trajectories of these intensities are organised around singularities, from the formation of the eye wall to that of thunderstorm cells, which unfurl according to a cascade of bifurcations (differentiation). At this point, the Idea of the hurricane is still only virtual, being purely intensive and topological. It has no extensive or geometric existence.
It is only when differenciation takes place that the virtual multiplicity of the hurricane is actualised into a discrete form. This differenciation is essentially nothing more than differentiation as it occurs in relation to actual, material conditions. The virtual Idea of a hurricane becomes a discrete multiplicity the moment that actual values (actual temperatures, actual pressures) are introduced. However, like we looked at in section one, continuous multiplicities are nothing more than structures that map processes. They explain how things come to be, but they don’t reflect the final product. When subjected to causality, there is thus a massive difference between virtual differentiation and its actual differenciation.
For Deleuze, it is the differenciation of intensities that gives rise to extensities and qualities. The height, width, and momentum of an actual hurricane are dependent on the interplay between pressure and temperature, which – in turn – are determined by causality and material conditions. It’s here that the quote on Bergsonian multiplicities from the last section becomes important: actualisation necessarily results in the production of spatialised, secondary qualities.
Morphogenesis: What is Philosophy?
“It is only in the zone of intensity that difference-driven morphogenesis comes into its own, and that matter becomes an active material agent, one which does not need form to come and impose itself from the outside.”
– Manuel DeLanda, Deleuze, Diagrams, and the Genesis of Form
To wrap up this article, I would like to return to DeLanda’s account of morphogenesis as it relates to multiplicities. Breaking the term down, morpho- designates form, whilst -genesis designates production. In other words, morphogenesis refers to the creation of forms. This is the heart of continuous multiplicities, which map the emergence of unfolding processes rather than stable identities. To go full circle, I want to end by tracking the morphogenesis of salt crystals, examining how it goes through differentiation and differenciation to be actualised.
Laying the groundwork for a salt crystal’s morphogenesis are six degrees of freedom: potential energy and kinetic energy with three possible spatial directions for each. As such, the virtual multiplicity that maps it has six dimensions. These dimensions are organised in turn by a myriad of singularities, such as that of a minimal point of energy. Differentiation, as a process defined by the progressive unfurling of singularities, develops the structure of this multiplicity by linking the rates of change of intensities together. Constantly, these intensities fall into trajectories organised around basins of attraction set up by the Idea’s singularities.
Eventually, differenciation takes hold as intensities approach the singularities that define the virtual multiplicity. A cascade of symmetry breaking transformations ensues, actual values being assigned in the process, in turn giving rise to geometric, extensive forms. The six dimensions of the salt-multiplicity gradually become specified as the process unfolds, the differential relations between kinetic and potential energy giving rise to an actual 3-dimensional structure. This is a process of morphogenesis because the virtual Idea of the crystal outlines a form, which is then actualised in a divergent manner.
Blackboard covered in differential equations
“[C]alculus is not a simple mathematical tool but the model for the genesis of every actual reality, including thought.”
– Anna Longo, Deleuze and Mathematics
At the heart of this morphogenesis is a dissimilarity between the virtual and actual. Even upon first glance, this is clear – we don’t experience the world in six dimensions, after all. This is how Deleuze is able to evade the trap of representation. There’s no distinction between what is possible and what is real, where the one is a representation of the other. Rather, there are two interrelated fields that are both equally real, neither of which reflects the other. To give an example of this, just look at making tea. Every actual instance of boiling water occurs through the differenciation of the same singularity – that of 100 degrees centigrade. However, this water isn’t equivalent to the intensive morphogenesis that gives rise to it. Rather, there is a fundamental difference in kind between the virtual and its actualisations.
As Deleuze once declared in an interview with his student Claire Parnet, philosophy is first and foremost a theory of multiplicities. These multiplicities – virtual and actual – are what make up our world. Although I only focused on physical phenomena, like the production of salt crystals or the formation of hurricanes, everything can be conceptualised through this framework based on intensities, the virtual, and the actual. Ethics, for instance, can be conceptualised as the analysis of how Ideas become actualised as virtues, epistemology can be thought of as the study of how knowledge becomes different/ciated, and so on. To close off, so far multiplicities have been defined as either virtual or actual. In fact, however, the two are always interacting – the one cannot exist without the other. As Deleuze and Guattari state in A Thousand Plateaus:
There is no question, however, of establishing a dualist opposition between the two types of multiplicities, [virtual] machines and [actual] machines, that would be no better than the dualism between the One and the multiple. There are only multiplicities of multiplicities forming a single assemblage, operating in the same assemblage: packs in masses and masses in packs. Trees have rhizome lines, and the rhizome points of arborescence. How could mad particles be produced with anything but a gigantic cyclotron? How could lines of deterritorialisation be assignable outside of circuits of territoriality? Where else but in wide expanses, and in major upheavals in those expanses, could a tiny rivulet of new intensity suddenly start to flow?
Further Reading and Main Bibliography
Bergson, Henri. Matter and Memory. Translated by Nancy Margaret Paul and W. Scott Palmer. New York: Zone Books, 1991.
———. La Pensée et le Mouvant : Essais et conférences. Paris: Presses Universitaires de France, 1934.
Boundas, Constantin V., ed. Deleuze and Philosophy. Edinburgh: Edinburgh University Press, 2006.
Buchanan, Ian. Assemblage Theory and Method: An Introduction and Guide. London: Bloomsbury Academic, 2021.
DeLanda, Manuel. Intensive Science and Virtual Philosophy. London: Bloomsbury Academic, 2013.
Deleuze, Gilles. Bergsonism. Translated by Hugh Tomlinson and Barbara Habberjam. New York: Zero Books, 1991.
———. Difference and Repetition. Translated by Paul Patton. New York: Columbia University Press, 1994.
———. Desert Islands and Other Texts 1953-1974. Translated by Mike Taormina. Los Angeles: Semiotext(e), 2004.
———. The Logic of Sense. Translated by Mark Lester. London: Athlone Press, 1990.
Deleuze, Gilles and Félix Guattari. A Thousand Plateaus: Capitalism and Schizophrenia. Translated by Brian Massumi. Minneapolis: University of Minnesota Press, 1987.
Parr, Adrian, ed. The Deleuze Dictionary: Revised Edition. Edinburgh: Edinburgh University Press, 2010.

Comments